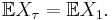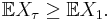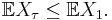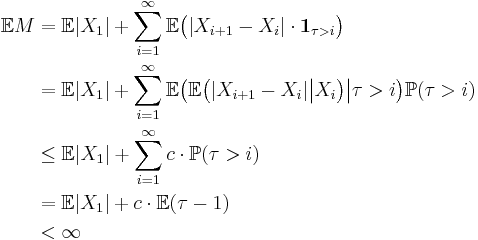Optional stopping theorem

In probability theory, the optional stopping theorem (or Doob's optional sampling theorem) says that, under certain conditions, the expected value of a martingale at a stopping time is equal to its initial value (and also expected value at any deterministic time). One version of the theorem is given below:

Let X₁, X₂, X₃, ... be a martingale and τ a stopping time with respect to X₁, X₂, X₃, ... . If

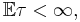
(a) $\mathbb{E}\tau<\infty,$

and

(b) there exists a constant c such that 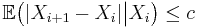$\mathbb{E}\big(\vert X_{i%2B1} - X_i \vert \big\vert X_i \big) \leq c$ a.s. for all i,

then

$\mathbb{E}X_{\tau}=\mathbb{E}X_1.$

Similarly, if X₁, X₂, X₃, ... is a submartingales or a supermartingales and the above conditions hold then

$\mathbb{E}X_{\tau}\geq\mathbb{E}X_1.$

for a submartingales, and

$\mathbb{E}X_{\tau}\leq\mathbb{E}X_1.$

for a supermartingales.

1 Applications
2 Proof
3 External links
4 References

Applications

The optional stopping theorem can be used to prove the impossibility of successful betting strategies for a gambler with a finite lifetime (which gives condition (a)) and a house limit on bets (condition (b)). Suppose that the gambler can wager up to c dollars on a fair coin flip at times 1, 2, 3, etc., winning his wager if the coin comes up heads and losing it if the coin comes up tails. Suppose further that he can quit whenever he likes, but cannot predict the outcome of gambles that haven't happened yet. Then the gambler's fortune over time is a martingale, and the time τ at which he decides to quit (or goes broke and is forced to quit) is a stopping time. So the theorem says that E[X_τ] = E[X₁]. In other words, the gambler leaves with the same amount of money on average as when he started. (The same result holds if the gambler, instead of having a house limit on individual bets, has a finite limit on his line of credit or how far in debt he may go, though this is easier to show with another version of the theorem.)^[1]

Suppose a random walk that goes up or down by one with equal probability on each step. Suppose further that the walk stops if it reaches 0 or m; the time at which this first occurs is a stopping time. If it is known that the expected time at which the walk ends is finite (say, from Markov chain theory), the optional stopping theorem predicts that the expected stop position is equal to the initial position a. Solving a = pm + (1 − p)0 for the probability p that the walk reaches m before 0 gives p = a/m.

Now consider a random walk that starts at 0 and stops if it reaches −m or +m, and use the Y_n = X_n² − n martingale from the examples section. If τ is the time at which it first reaches ±m, then 0 = E[Y₁] = E[Y_τ] = m² − E[τ]. This gives E[τ] = m².

Care must be taken, however, to ensure that all the conditions of theorem hold. For example, suppose the last example had instead used a 'one-sided' stopping time, so that stopping only occurred at +m, not at −m. The value of X at this stopping time would therefore be m. Therefore, the expectation value E[X_τ] must also be m, seemingly in violation of the theorem which would require E[X_τ]=0. The failure of the optional stopping theorem shows that the expected time for the random walk to exceed any non-zero level must be infinite.

Proof

Assume the conditions in the version given above and let 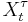$X_t^\tau$ denote the stopped process. This is also a martingale (or a submartingale/supermartingale accordingly). Obviously it converges to 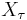$X_\tau$ almost surely. Now writing the stopped process as

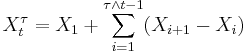
$X_t^\tau=X_1%2B\sum_{i=1}^{\tau \and t-1}(X_{i%2B1}-X_i)$

gives

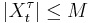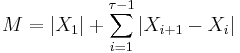$|X_t^\tau|\leq M$ where $M=|X_1|%2B\sum_{i=1}^{\tau-1}|X_{i%2B1}-X_i|$ .

Now by the monotone convergence theorem

$\begin{align}\mathbb{E}M &=\mathbb{E}|X_1|%2B\sum_{i=1}^\infty \mathbb{E}\big(|X_{i%2B1}-X_i|\cdot\mathbf{1}_{\tau>i}\big)\\ &=\mathbb{E}|X_1|%2B\sum_{i=1}^\infty \mathbb{E}\big(\mathbb{E}\big(|X_{i%2B1}-X_i|\big|X_i\big)\big|\tau>i\big)\mathbb{P}(\tau>i)\\ &\leq\mathbb{E}|X_1|%2B\sum_{i=1}^\infty c\cdot\mathbb{P}(\tau>i)\\ &=\mathbb{E}|X_1|%2Bc\cdot\mathbb{E}(\tau-1)\\ &<\infty\\\end{align}$

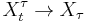so since $X_t^\tau\rightarrow X_\tau$ a.s., by the dominated convergence theorem 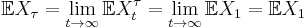$\mathbb{E}X_\tau=\lim_{t\rightarrow\infty}\mathbb{E}X_t^\tau=\lim_{t\rightarrow\infty}\mathbb{E}X_1=\mathbb{E}X_1$ . Similarly, the appropriate inequality is reached for a submartingale/supermartingale by changing the middle equality to an inequality.

External links

Doob's Optional Stopping Theorem

References

^ http://www.scribd.com/doc/28125042/Unit-Betting-System

Optional stopping theorem

Contents

Applications

Proof

External links

References